Table of Contents
Computational and generative design sit at the intersection of mathematics, computer science, and design. While advanced mathematical concepts certainly have their place, there are fundamental mathematical building blocks that form the core toolkit for most computational design work. This article outlines 10 essential concepts that every computational designer should master.
Vector Mathematics
At the heart of computational design lies vector mathematics! Vectors are the fundamental building blocks for describing position, direction, and movement in both 2D and 3D space. Understanding vector operations is crucial for:
- Translation and transformation of geometric elements
- Calculating distances and directions
- Implementing particle systems and dynamic behaviours
- Defining surface normals and orientation
Key vector operations include addition, subtraction, dot product, and cross product. The dot product is particularly useful for calculating angles between vectors, while the cross product helps determine perpendicular vectors and surface normals. Check this article on points and vectors in computational design to learn more about these operations.
Applied Example: In facade design, vectors are essential for creating sun-shading systems. By calculating the angle between the sun vector and facade normal vector using dot products, designers can determine the optimal angle for kinetic shading panels. This has been implemented in projects like the Al Bahar Towers in Abu Dhabi, where hexagonal shading units adjust their position based on vector calculations of sun angles.

Al Bahar Tower – Facade structural detailing
Al Bahar Tower – Reactive facade mechanism
Linear Transformations
Linear transformations allow designers to manipulate geometric objects systematically. Understanding transformation matrices enables:
- Scaling, rotation, and translation of objects
- Proper composition of multiple transformations
- Implementation of perspective and orthographic projections
- Creation of complex geometric patterns through repeated transformation
The concept of transformation matrices as linear operators provides a unified framework for handling all types of geometric transformations. Watch this excellent video by Khan Academy to visualize this concept!
Applied Example: In digital fabrication, transformation matrices are crucial for robotic arm control in large-scale 3D printing. The 2024 ICD/ITKE Research Pavilion used transformation matrices to coordinate multiple robotic arms printing a fiber-reinforced polymer structure. Each robot needed to understand its position relative to both the global coordinate system and other robots, requiring precise transformation calculations.
ICD Pavillion – Truss layout system
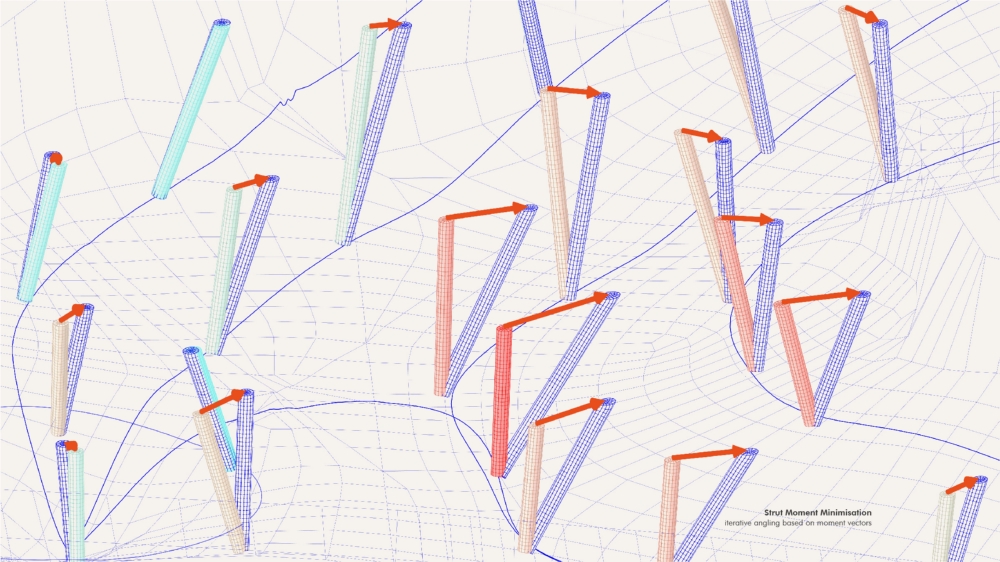
ICD Pavillion – Transformation of structural trusses
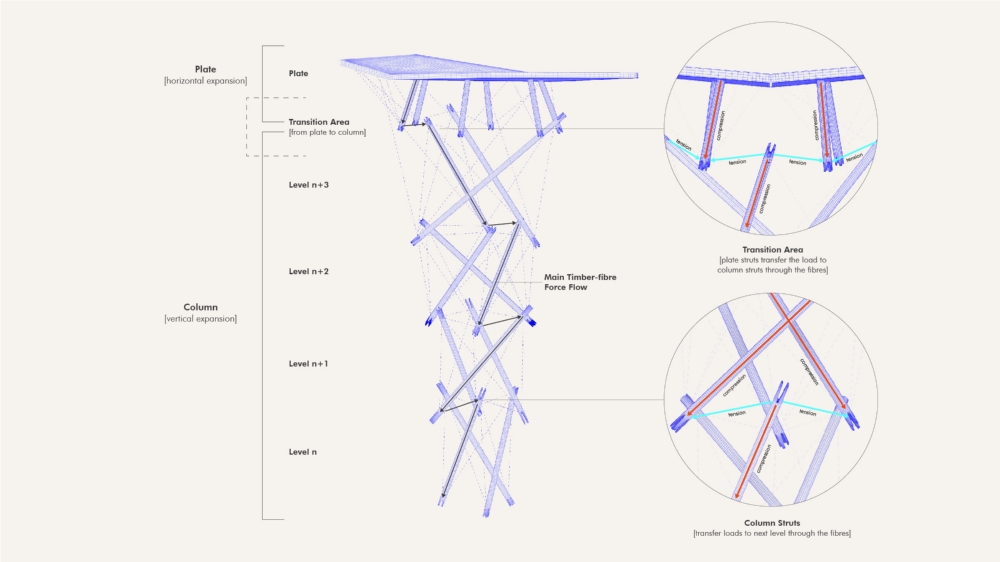
ICD Pavillion – Force flow and horizontal section
Parametric Equations
Parametric equations are essential for creating and manipulating curves and surfaces. They provide:
- Mathematical description of curves (lines, circles, splines)
- Control over complex geometric forms through parameters
- Foundation for implementing NURBS and other curved surfaces
- Tools for animation and motion design
Understanding how to work with parameters and their ranges allows designers to create dynamic, adjustable geometric systems. This article explains how parametric equations are used to create simple geometric shapes, such as an ellipse.
Applied Example: The Beijing National Stadium (Bird’s Nest) utilized parametric equations to define its complex steel structure. The primary structure was generated using parametric curves that responded to structural load analysis, while maintaining aesthetic requirements. The fabrication process required precise mathematical descriptions of each unique steel member’s geometry.
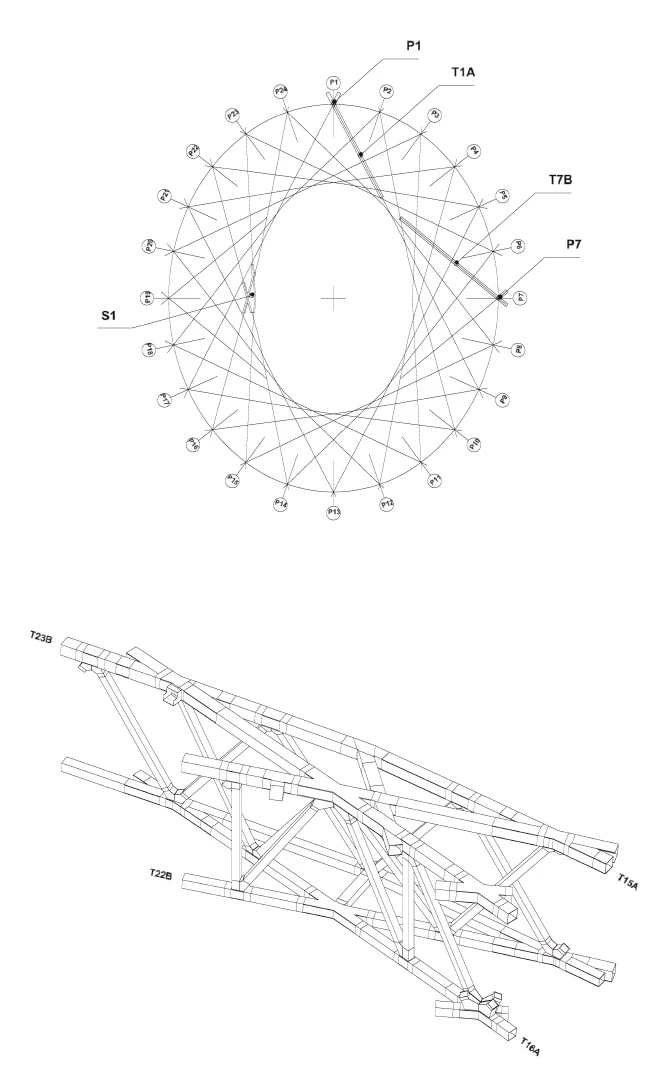
Bird’s Nest Stadium – Steel member layout and connections
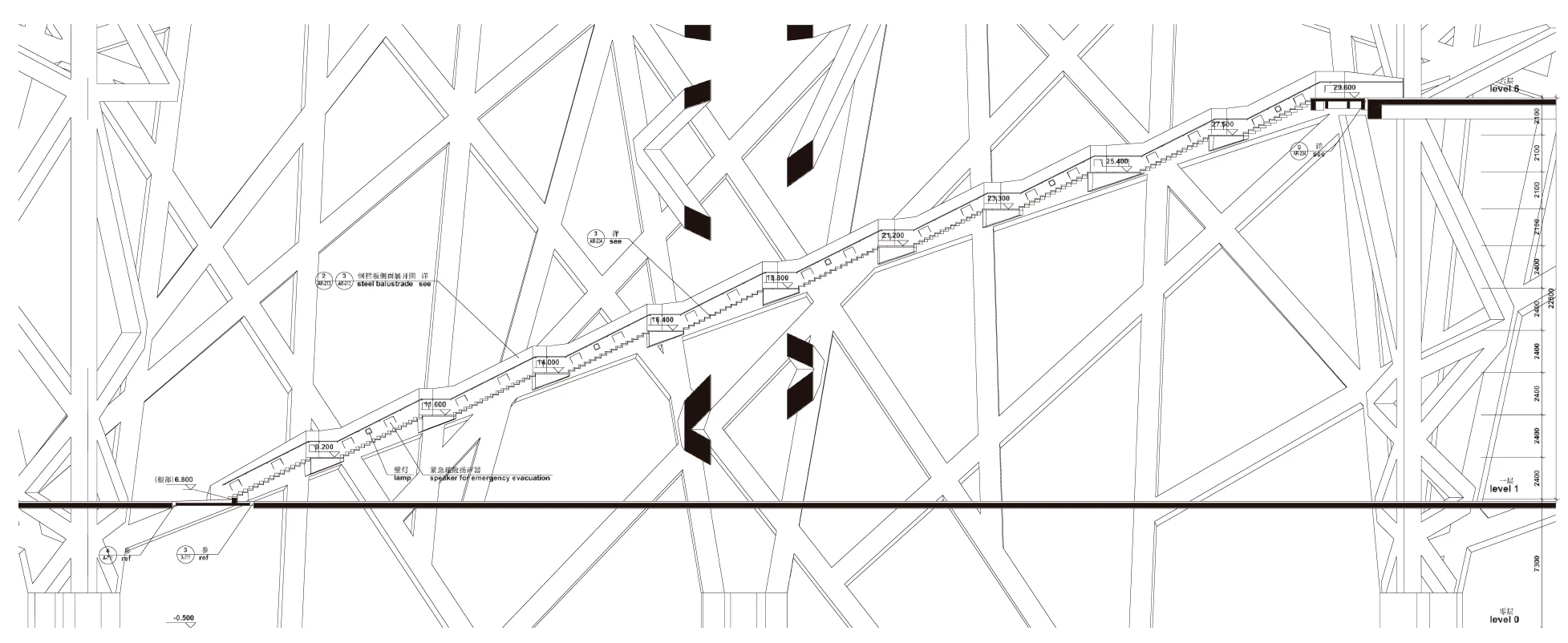
Bird’s Nest Stadium – Elevation and steel member details
Trigonometry
While seemingly basic, trigonometric functions are indispensable in computational design for:
- Calculating angles and distances
- Creating circular and periodic motions
- Generating wave-like patterns and behaviours
- Implementing rotations and angular measurements
The ability to think in terms of sine, cosine, and tangent functions opens up possibilities for creating organic, flowing designs. Here is a real life example of using tangents for calculating roof overhang.
Applied Example: In acoustic panel design, trigonometric functions help create diffusion patterns. Acoustic analysis uses sine-based well depth sequences to scatter sound waves effectively. The manufacturing process requires precise calculation of each well’s depth using trigonometric relationships to achieve specific acoustic properties.
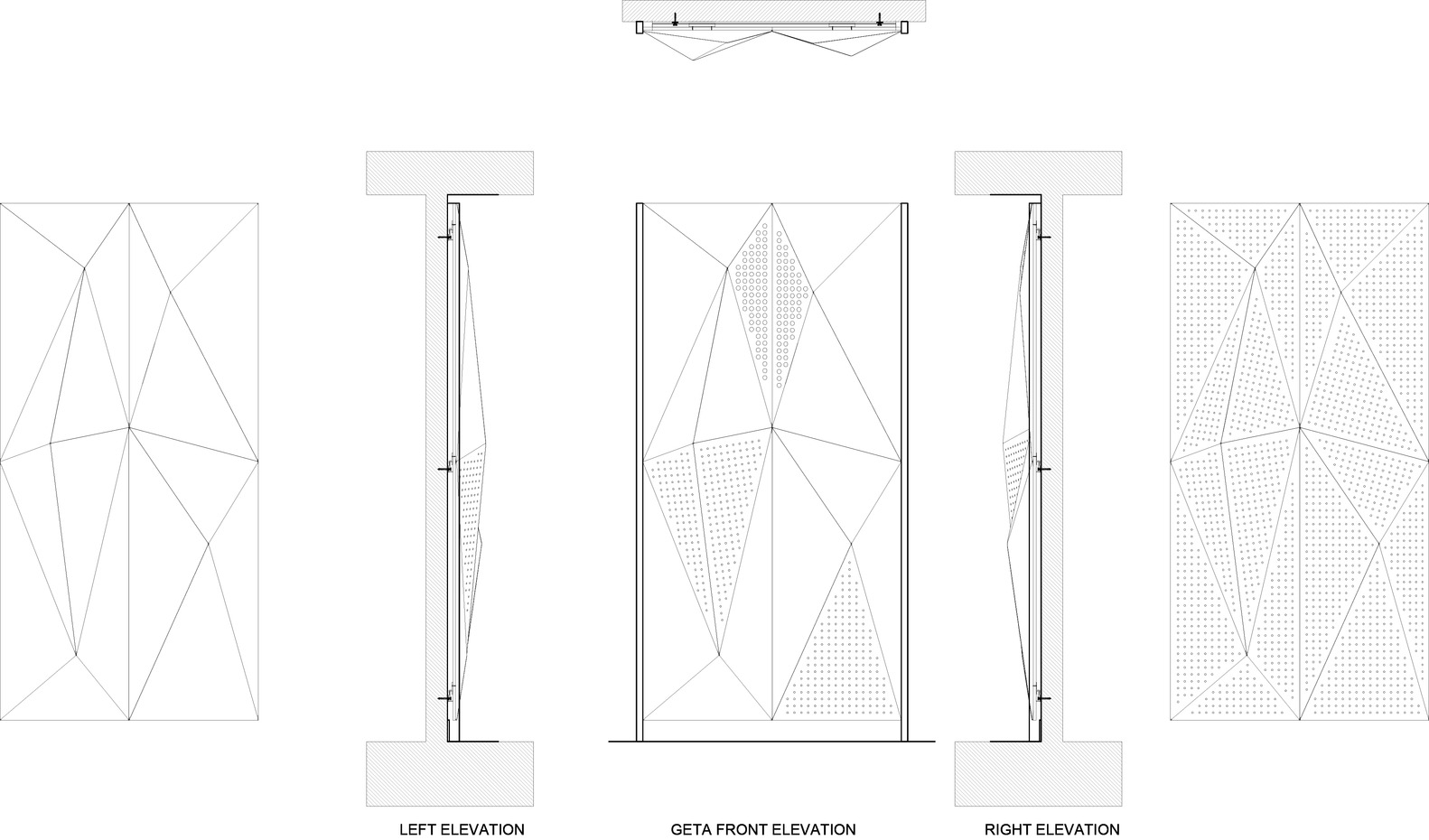
Acoustic panel fabrication – Elevation drawings and details
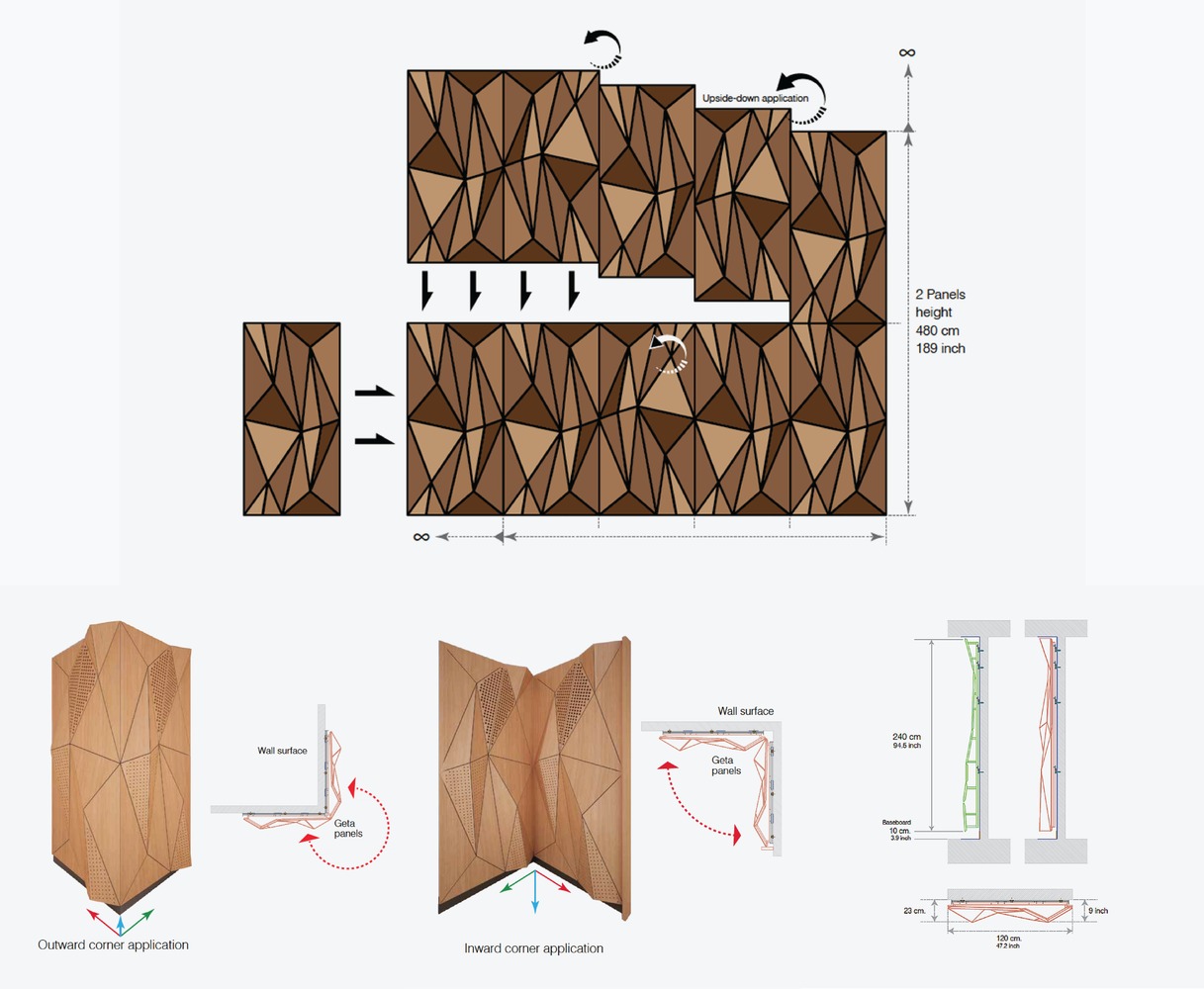
Acoustic panels – Arrangement and materiality
Acoustic panels – Elevation drawing and measurements

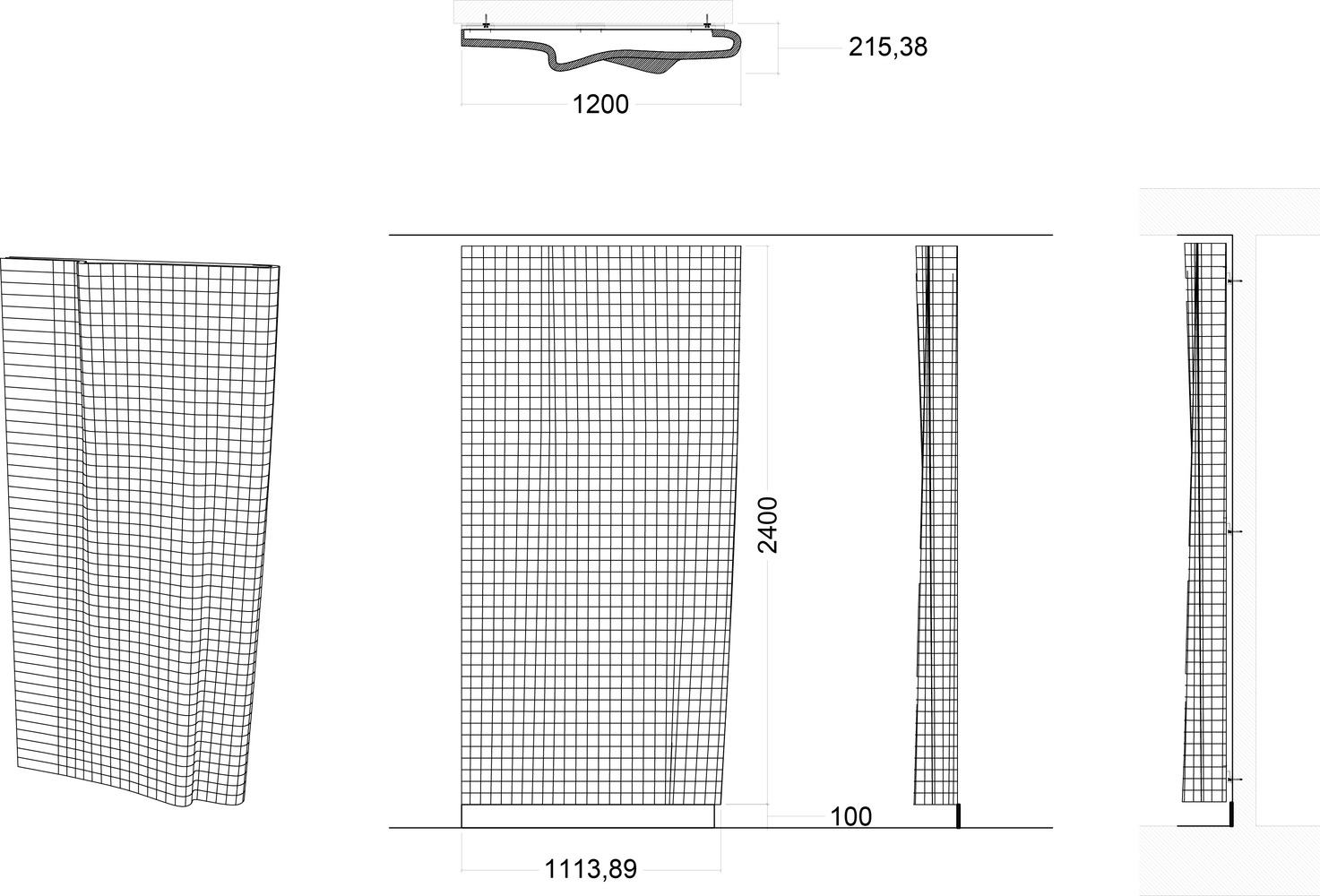
Acoustic panels – Renders, arrangement and context
Interpolation
Interpolation is crucial for creating smooth transitions and blending between states:
- Linear interpolation (lerp) for basic transitions
- Easing functions for natural motion
- Color space interpolation
- Shape morphing and animation
Understanding different interpolation methods helps create more natural and aesthetically pleasing transitions. Read these lecture slides from University of Toronto to learn more about interpolating curves.
Applied Example: The Morpheus Hotel in Macau uses interpolation in its exterior structural system. The exoskeleton’s complex geometry was generated by interpolating between different structural conditions at each level, creating a smooth transition that maintains structural integrity while achieving its distinctive aesthetic.

Morpheus Hotel – Section drawing
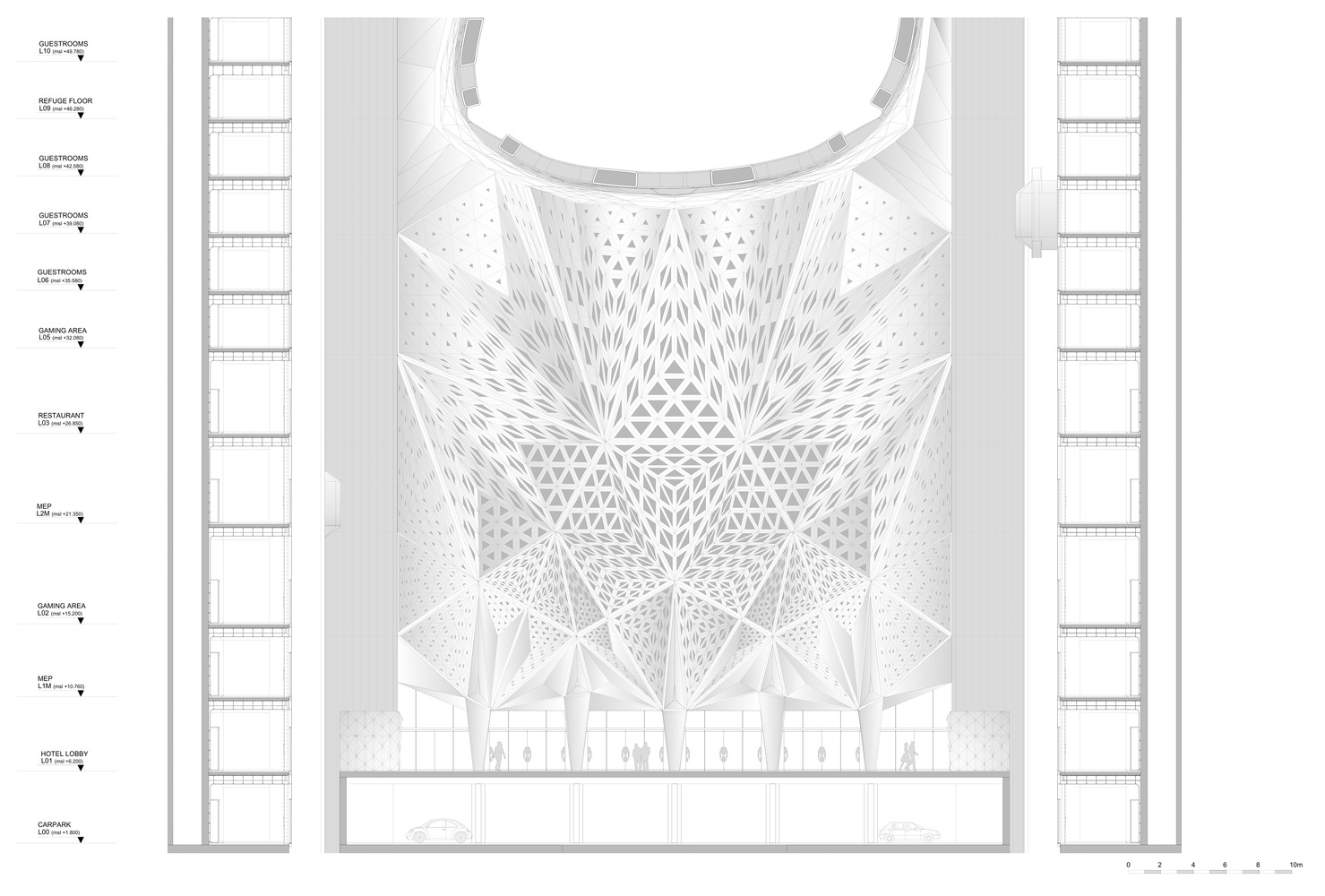
Morpheus Hotel – Detailed section with truss system

Morpheus Hotel – Facade details, elevation photograph
Coordinate Systems
Mastery of different coordinate systems enables designers to work effectively in various contexts:
- Cartesian coordinates for precise positioning
- Polar coordinates for radial patterns
- UV coordinates for texture mapping
- Local vs. global coordinate spaces
The ability to transform between coordinate systems is often key to solving complex design problems. Read this very informative and graphic introduction to coordinate systems and how they relate to the AEC industry from E-verse!
Applied Example: In digital wood fabrication, coordinate system transformations are crucial for multi-axis CNC milling. The Tallinn Architecture Biennale installation “Digital Thicket” ” required continuous translation between the machine’s coordinate system and the material’s grain direction coordinate system to achieve optimal cutting paths while respecting wood grain structure.

Digital Thicket – Final combination system and joinery
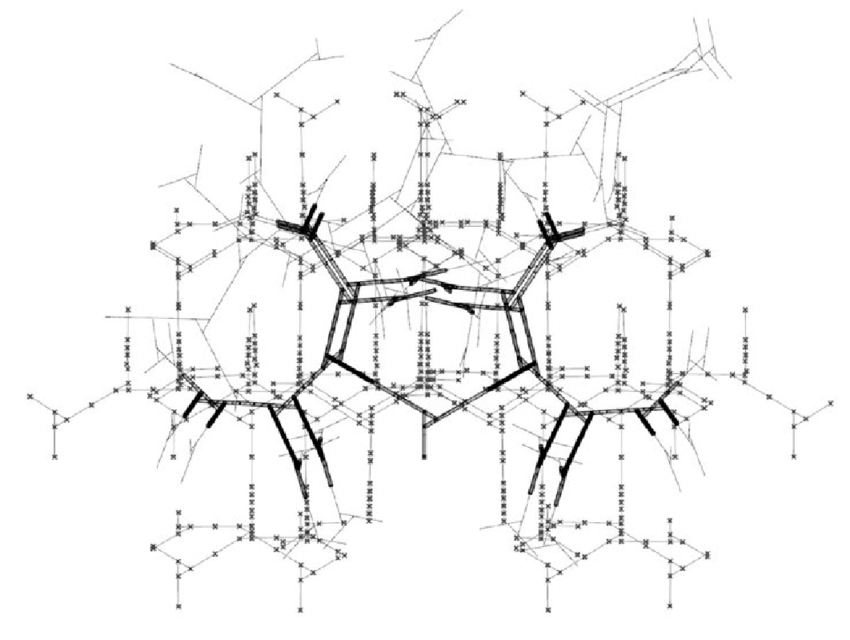
Digital Thicket – Coordinate system plotting and layout

Digital Thicket – Final product in environmental context
Probability and Randomness
Controlled randomness adds organic qualities to computational designs:
- Random distribution patterns
- Noise functions for natural variation
- Weighted randomness for controlled chaos
- Probability-based decision making
Understanding how to generate and control random elements allows for more natural-looking designs while maintaining artistic control. Have a further look at this paper that ties probability in to data-driven design.
Applied Example: The Louvre Abu Dhabi’s dome uses controlled randomness to create its famous “rain of light” effect. The perforation pattern was generated using probability distributions to create varying densities of openings, resulting in natural-looking light patterns while maintaining structural requirements.

Louvre Abu Dhabi – Light diffusion structure and details

Louvre Abu Dhabi – Rain of Light distribution and close-up

Louvre Abu Dhabi – Jean Nouvel – Photograph of completed project
Modular Arithmetic
Modular arithmetic is essential for:
- Creating repeating patterns
- Managing cyclic behaviours
- Implementing wrapping effects
- Controlling animation loops
This concept is particularly useful when working with finite spaces or creating periodic behaviours. While this seems to be quite a basic mathematical concept, it is quite important even when you play with simple concepts like linear array and polar array. You may learn more about these concepts of Modular Arithmetic from Brilliant.org!
Applied Example: In brick facade design, modular arithmetic helps manage complex patterns. The Siemens Headquarters in Masdar City uses a parametric brick pattern where the rotation of each brick is determined by modular arithmetic, creating a repeating pattern that optimizes shading while maintaining constructability.
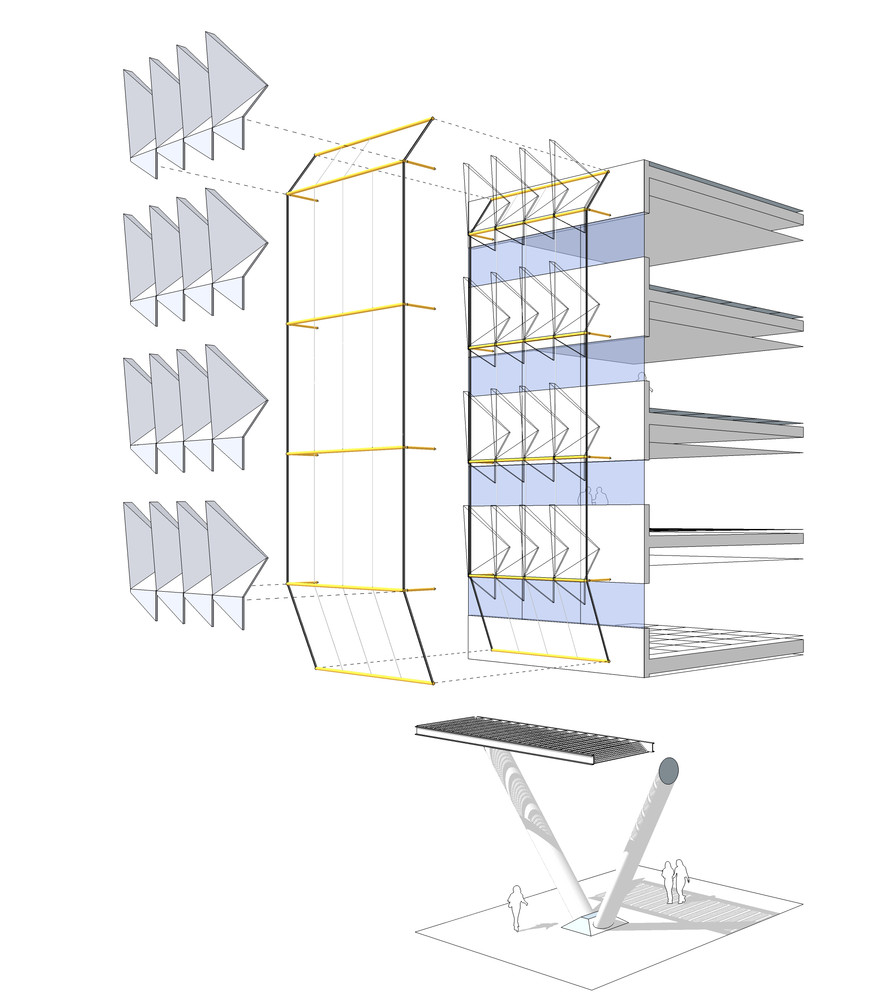
Siemens (Masdar City) – Facade structural system and components
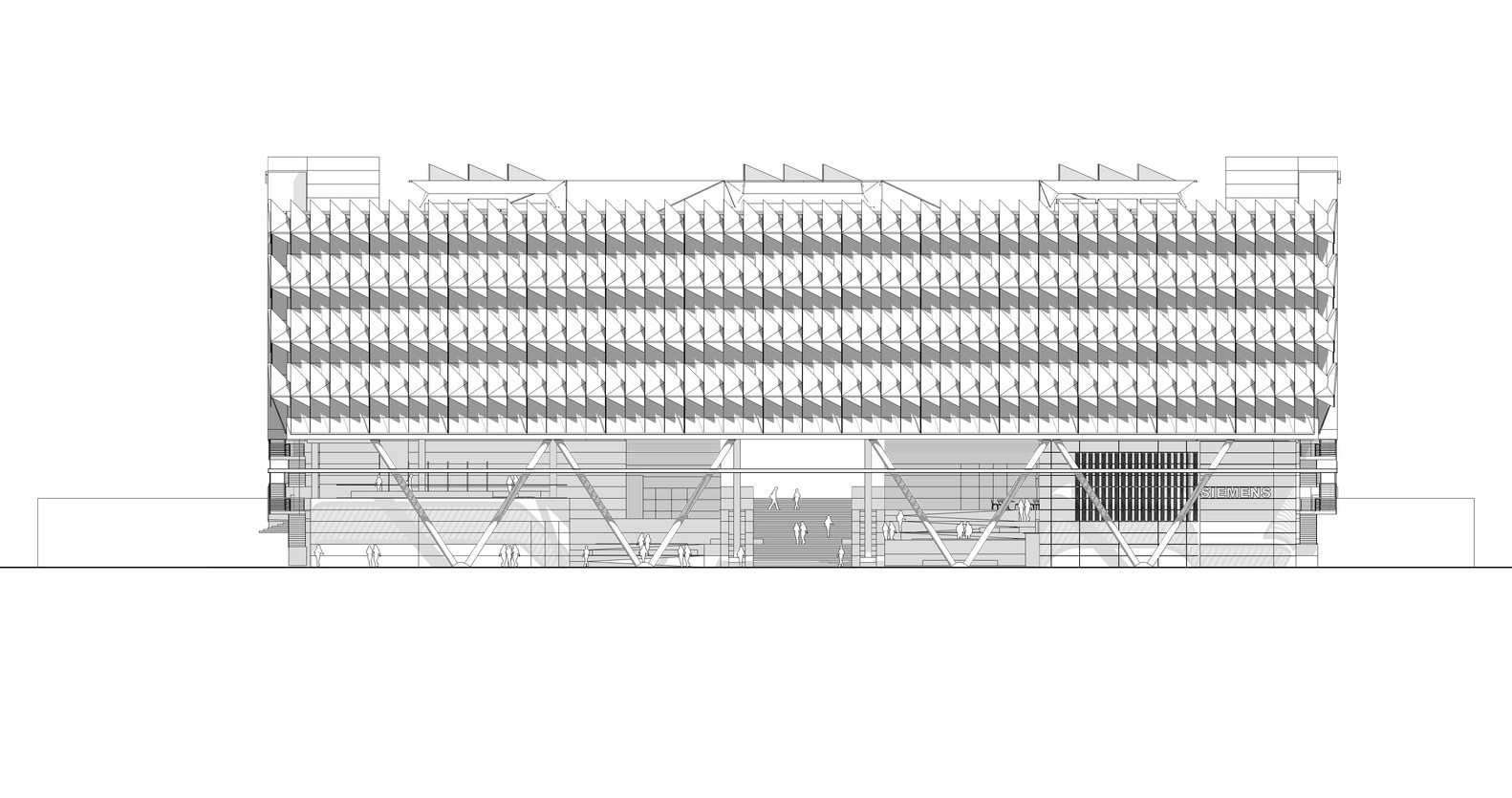
Siemens (Masdar City) – Elevation drawing

Siemens (Masdar City) – Facade detailing

Siemens (Masdar City). – Completed facade
Graph Theory
Understanding basic graph theory helps in:
- Creating network visualizations
- Implementing path-finding algorithms
- Analyzing spatial relationships
- Generating organic patterns through L-systems
While not strictly mathematical, graph theory’s mathematical foundation is crucial for many generative design applications. Here is a short excerpt of an article explaining graph theory’s use in space planning.
Applied Example: In space planning, graph theory is used for circulation optimization. Designers now, from the smallest of houses to the largest of stadiums, have used graph theory algorithms to optimize visitor flow through its various types of layouts, ensuring efficient movement patterns while maintaining the desired architectural experience.
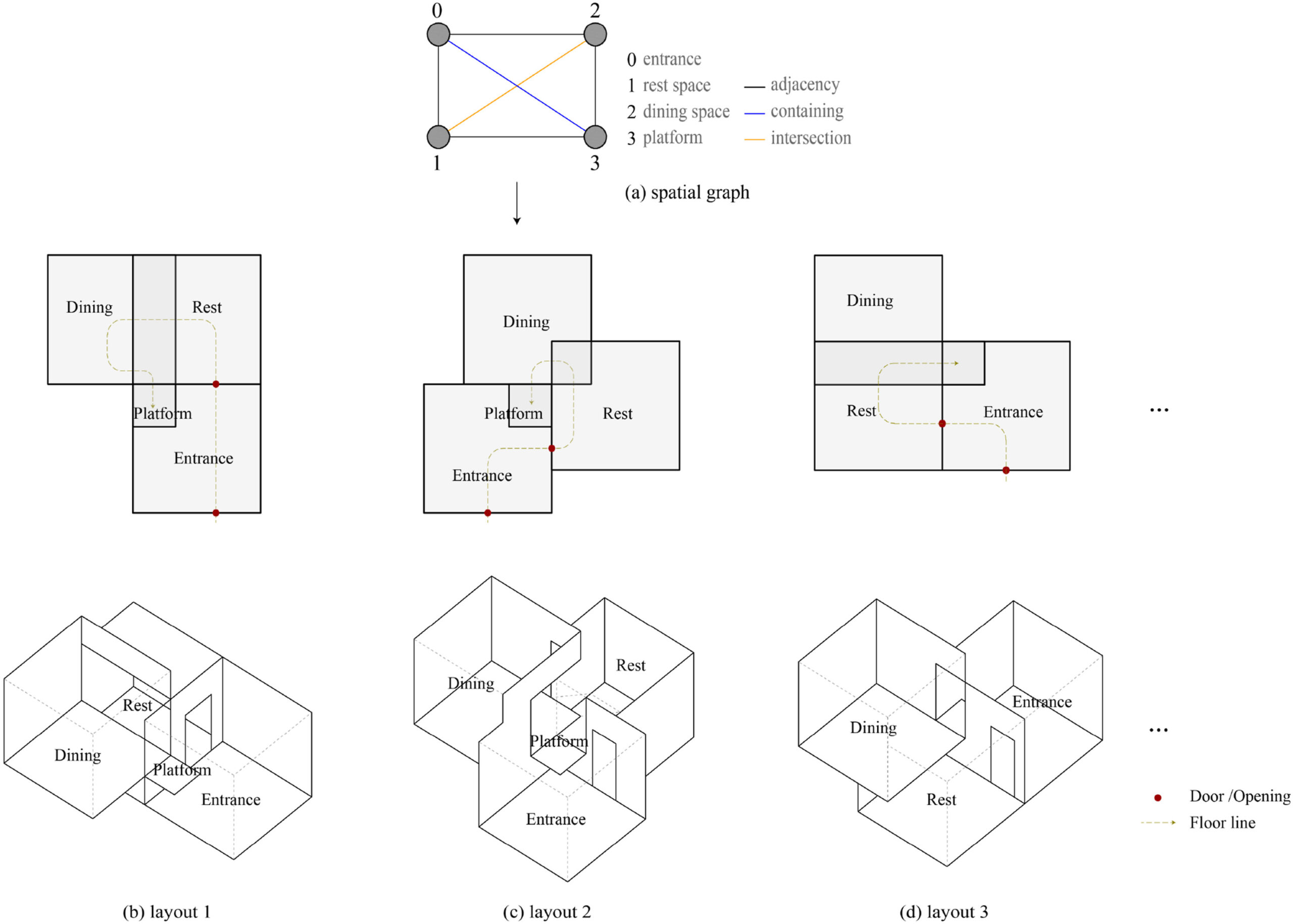
Graph layouts and permutations for space planning
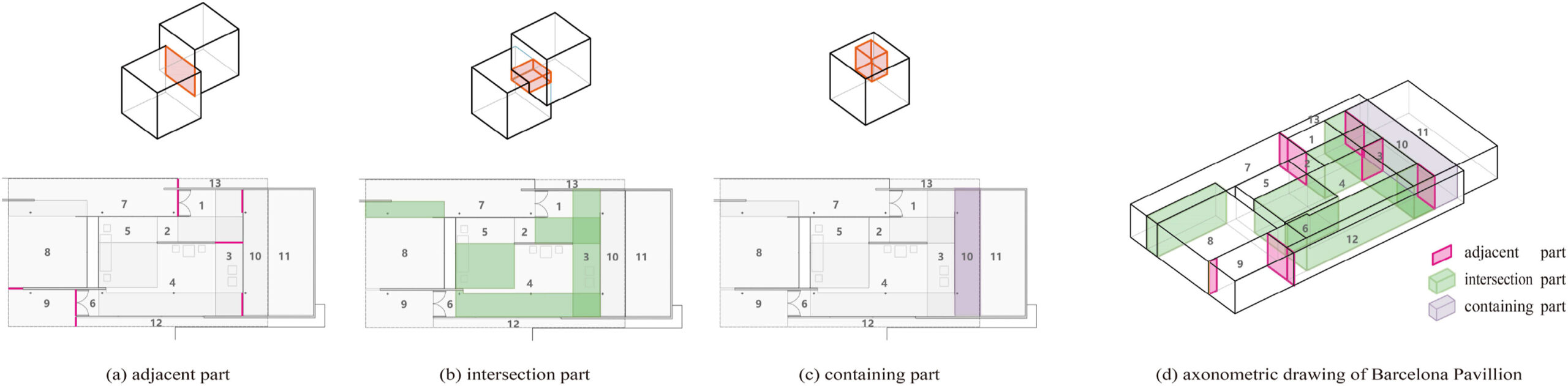
Graph representation and intersections of Barcelona Pavillion
Optimization for Generative Design
Understanding optimization principles helps in:
- Solving layout problems
- Implementing responsive designs
- Creating efficient generative systems
- Managing competing design objectives
The ability to frame design problems in terms of constraints and optimization goals is invaluable for creating robust computational design systems. For an in-depth exploration of architecture design optimization, click here to read a survey paper.
Applied Example: In structural optimization, the Qatar National Convention Centre’s iconic facade structure was developed using topology optimization algorithms. The design balanced multiple constraints including structural efficiency, material usage, and aesthetic requirements, resulting in its distinctive tree-like appearance.

Qatar National Convention Center – Details of bifurcated support structure

Qatar National Convention Center – Photographed final facade
These fundamental concepts can help emerging computational designers to tackle a wide range of design challenges with a new depth, leading to more thorough and systematic solutions. The key is not just understanding these concepts in isolation, but recognizing how they can be combined and applied to solve real-world design problems.
At BeeGraphy, we routinely organize workshops and tutorials on computational and parametric design. We encourage you to follow our YouTube channel for the latest updates and resources on how to apply these mathematical concepts to your next computational design project.