BeeGraphy에서의 벤 다이어그램

Table of Contents

BeeGraphy에서의 벤 다이어그램

칸토어 “수학의 본질은 그 자유로움에 있다”

“수학의 본질은 그 자유로움에 있다”(Das Wesen der Mathematik liegt in ihrer Freiheit) 현대 수학의 기본이 되는 집합론을 창시한 게오르그 칸토어(Georg Cantor)의 이야기이다.

GEORG CANTOR (출처)

무슨 뜻일까? 수학이 자유롭다? 가장 논리적로 엄밀한 학문인 수학에서조차 우리가 일반적 로 받아들이는 것들은 신이 정해준 절대적이고 불변의 기준이 아니라 단지 인간들의 약속에 의 한 것로 논리성만 유지된다면 얼마든지 자유롭게 사용할 수 있다는 것이다. MathDesigner의 교실에서는 이 자유로움로 얼마든지 상상하면서 즐겁게 수학문제를 해결할 수 있다.

우리는 수학로 예술을? 아니 예술로 수학을 하고 있다고 생각한다.

이번 시간에는 집합 단원에 나오는 벤다이어그을 BeeGraphy를 이용해 그 원리를 이해하고 또 재미있는 작업을 해보려고 한다.

집합에 등장하는 멋진 그림을 하나 소개한다. “벤 다이어 그!”

벤다이어그은 여러 개의 원이 겹쳐진 형태로 이루어 진다. 각 원은 하나의 집합을 나타낸다(집 합은 서로 다른 원소들의 순서 없는 모음이다.)

1880년 존 벤에 의해 도입된 논리학의 시각적 도구 벤다이어그이다. 보통 두 개 혹은 세 개 의 원로 된 벤다이어그을 많이 볼 수 있다. 원의 공통부분은 각 원 안에 속해 있는 원소가 공통적로들어있음을 의미한다. A라는 집합에 1,2,3,4가 들어있고, B라는 집합에 2,4,5가 있 며 2,4는 두 집합 모두 속해있는 원소라는 논리관계를 단순한 원을 이용해 누구라도 쉽게 이해 할 수 있도록 표현하는 도구이다.

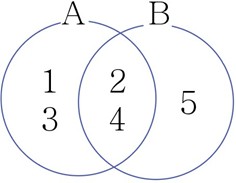
집합 A = {1,2,3,4}

집합 B = {2,4,5}

여기서 2와 4는 집합 와, 집합 에 모두 들어 있다. 한 원을 A, 다른 원을 B라고 하면 공통 원소 2와 4는 겹치는 영역에 속한다. 원 두 개만로도 누구나 집합들이 서로 어떻게 관련되는지 한눈에 이해할 수 있다.

집합 (원)이 하나라면 몇 개의 영역을 나타낼 수 있을까? 정답은 2개다~

-원 안

-원 밖

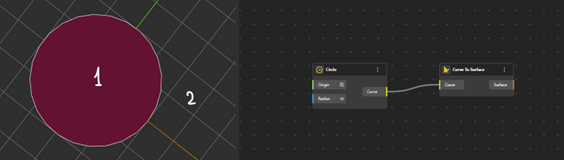
원을 하나 더 추가하면 이제 두 집합이 되고, 영역의 수는 네 개로 늘어난다. 딩동댕~ 정확하다.

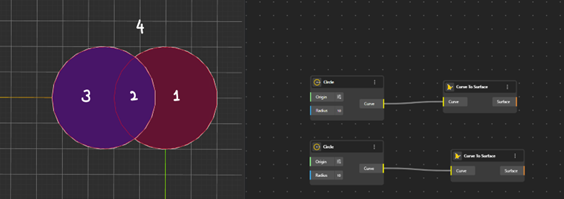
그렇다면 집합(원)의 개수가 늘어나면 어떻게 될까?

n 개의 집합이 만들어 내는 영역의 수는 ^( 집합의 개수)로 표현할 수 있다. 예를 들어

1개의 집합: ^ 개의 영역 (집합의 안 & 밖)
2개의 집합 ^  개의 영역 (두 집합에 대해 안과 밖로 만들 수 있는 모든 조합)
3개의 집합 ^ 개의 영역
4개의 집합 ^ 개의 영역 등등…

따라서 , 집합의 수가 늘어날수록 표현할 수 있는 영역의 개수는 거듭제곱(^)로 늘어난다.

세 개의 집합 이상로 벤다이어그을 확장하기

세 집합에 대한 벤다이어그은 쉽게 그릴 수 있지만, 집합의 수를 늘리면 어떻게 될까? 시각적로 이를 표현할 때 BeeGraphy가 유용해 진다.

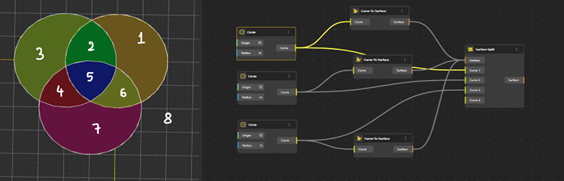
방법은간단하다.

앞서만든3개의집합에대한벤다이어그에서시작할것이다.각영역에점을하나씩찍고,그점을겹치거나반복되지않도록꼭한번만지나갈수있도록점과점을연결하도록한다.처음에는조금낯설어보이겠지만아래그림에서빨간색선로그려진영역이4번째집합을표현한것이다.자,4개의집합에대한벤다이어그이완성되었다.

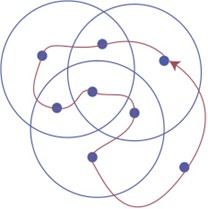
4개의 원을 이용한 벤다이어그의 기하학적 한계

원 2개나 3개 에서는 학생들이 눈로 쉽게 영역을 확인할 수 있어 벤다이어그의 영역의 수 를 세거나 이해하는 것이 어렵지 않다. 그러나 원이 4개가 되면 ^ 개의 영역을 표현해야 하고 그 중 일부는 기존의 방법로 그리기에 한계가 있다. 일부가 숨겨져 있거나 모양이 불규 칙하기 때문에 눈로 일일이 세기가 까다로워지는 것이다.

학생들에게 먼저 4개의 원로 벤다이어그을 그리라고 하면 처음에는 단순하고 쉽게 생각하고 대답한다. “ 원을 하나만 그리면 되자나? ”

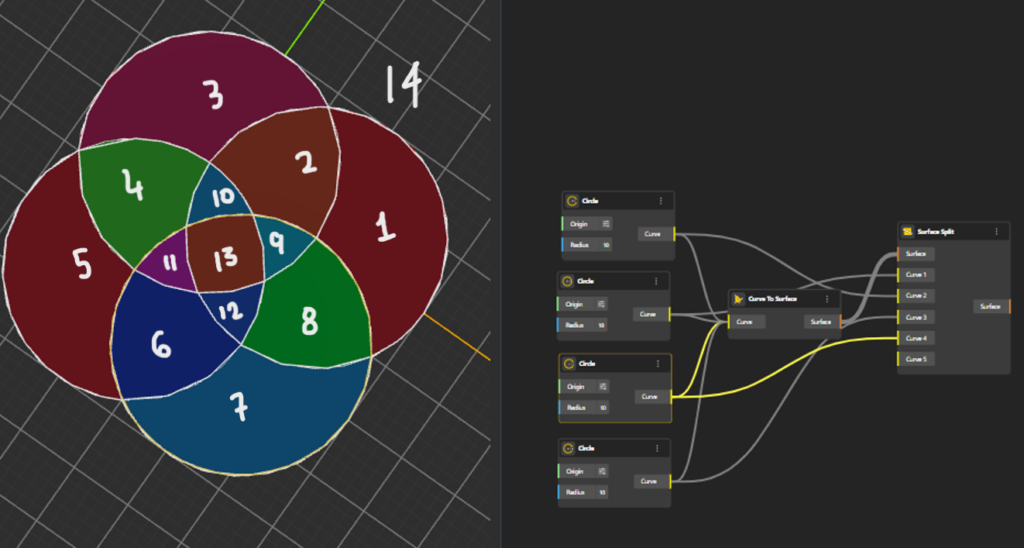
하지만, 실제 그리면서 어려움을 호소하고 의문을 갖게 된다. 학생들은 네 개의 원을 여러 방식

로 배치해 보고 또 그럴듯해 보이기도 하지만 곧 모순점을 발견하게 된다. 벤다이어그이 대 칭적이거나 미적로 좋을 수도 있지만, 실제로 영역을 세어보면 16개가 아니라 14개나 15개만 표현할 수 있는 것이다.

왜 이런 일이 생기는 것일까?

완벽한 원 네 개는 서로를 올바른 방식로 겹치지 않도록 모두 교차시키는 것이 어렵기 때문이 다.

어떤 원은 다른 원과 두 번 교차하지 않는다.
일부 교차된 부분이 잘못 겹쳐진다.
학생들이 인지하지 못한 몇 개의 영역이 중복되어 겹쳐진다.

따라서 완벽한 원 4개로 그리는 방법은 제대로 작동하지 않는다.

진짜 4개의 집합을 표현하는 벤다이어그은 A,B,C,D 영역이 안과 밖에서 만들 수 있는 16개의 조합이 모두 중복되지 않도록 표현되어야 하는 것이다.

4개의 집합을 벤다이어그로 완벽하게 표현하기 위한 접 근법

오래 전 수학자들은 완벽한 원 4개로 16개의 영역을 표현할 수 있는 벤다이어그을 그릴 수 없다는 것을 발견했다. 따라서 16개의 영역을 표현할 수 있는 가장 좋은 방법은 다음과 같다.

3개의 원로 만든 벤다이그에서 시작 : 이미 8개의 영역이 표현되어 있다.
각 영역에 점(여기선 무게중심 centroid)을 찍기 : 모든 영역에 점을 하나씩 찍는다.
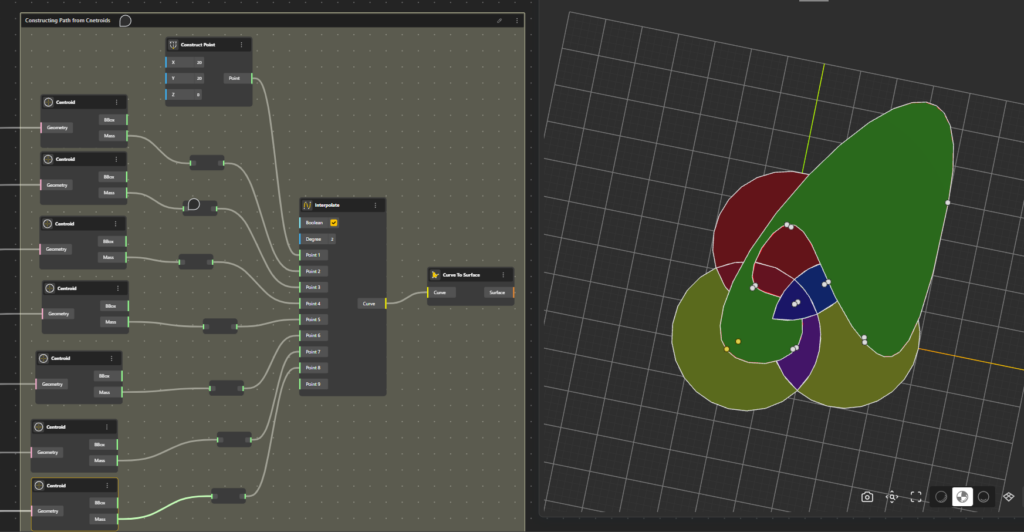
4번째 집합을 표현하기 위해 각 점들을 겹치지 않도록 차례대로 연결한다. (아래그림 참고) (각 영역에 찍은 점을 정확히 한번씩만 지나고 8개의 영역을 차례로 연결하면서 16개의 영역 이 만들어지지 확인한다)

위와 같은 불규칙한 고리 모양의 4번째 집합은 완벽한 원 모양은 아니지만 수학적로 오류가 없는 벤다이어그을 표현할 수 있다.

4번째 집합을 표현한 원리는 다음과 같다.

기존의 모든 영역을 정확히 분할하고
어떤 영역도 빠뜨리지 않며
중복되지 않도록 연결한다.

이와 같은 방법로 학생들은 정확히 16개 영역을 표현할 수 있는 4번째 집합을 벤다이어그

로 표현할 수 있다.

위 이론이 더 궁금하다면 아래 링크를 참고해 보도록 하자.

원 4개로 왜 벤다이어그을 만들 수 없을까?

medium.com/@danyaLtairoski/why–you-cant-make-a-venn-diagram-with-4-circLes-bea3c2dcbc5d

원 4개로 벤다이어그을 그릴 수 없는 이유와 해결방법

www.quora.com/Why-cant-we-draw-a-Venn-diagram-for-4-sets-with-circLes-and-how-can-we-soLve-it

BeeGraphy로 4번째 벤다이어그 만들기

자, 이제 BeeGraphy를 이용해 이 구조를 시각화 해보도록 하자. 그렇다면,

왜 BeeGraphy 일까?

학생들이 직접 시각화 작업을 해보면 그 아이디어의 아름다움을 실제로 느낄 수 있다. 딱딱한 수학적 개념을 손로 느낄 수 있는 유의미한 경험로 바꿔줄 수 있는 것이다.

수학적 원리에 대한 시각화 작업에 디자인씽킹 방법론을 적용하기 자, 이 문제를 디자인씽킹 방법론을 이용해 정리해보자.

정의(Define) : “ 네 개 이상의 집합을 어떻게 효과적로 시각화할 수 있을까? ” 라고 자신 에게 물어보자. 이는 학생들이 교과서 너머의 다양한 접근을 탐색할 수 있는 기회를 제공한다.
발상(Ideate) : 세 개의 원에 대해 (Centroid 노드블록을 사용) 각 영역에 점을 찍고 각 점 마다 번호를 부여하고 순서대로 연결한다. 이때, 중요한 점은 선이 중복되지 않고 모든 영역을 한 번씩 지나가도록 하는 것이다. 이 과정을 통해 학생들은 평면이 분할 될 때 만들어질 수 있는 최대 영역의 개수를 구할 수 있는 일반화된 원리를 자연스럽게 습득할 수 있다. 문제해 결을 위한 발견은 암기가 아니라 탐구하는 과정에서 일어난다.
프로토타입(Prototype) : BeeGraphy의 노드블록(Circle, Curve to Surface, Centroid, List Item, and others)를 사용해 학생들은 자신만의 다이어그을 만들고 반복적로 수정 보완하며 수학적 원리를 습득할 수 있게 된다.

파라메트릭디자인로 수학원리를 시각화하기

파라메트릭디자인 방법론을 이용해 학습자는 수학적 원리를 시각과 할 수 있다. 즉, 수학적 원리 와 표현을 상호작용의 방법을 통해 수학 문제 해결방법에 대한 이해를 도울 수 있다. 파라메트 릭디자인 방법론을 이용해 학생들은 수학문제에서 변수 등을 조절해 보며 어떠한 변화가 일어나 는지 직접 관찰하고 느낄 수 있는 것이다. 결과적로 기하, 대수 뿐만 아니라 무엇보다 수학적 원리를 스스로 구성하고 사용하면서 문제해결을 위한 창의적인 방법을 생각해 낼 수 있는 능력 을 갖출 수 있다. 이러한 이해는 메타인지를 활용한 접근법과 시각화 작업의 긍정적인 결과라고 할 수 있다. 이것이 BeeGraphy의 강점이라고 하겠다.

집합 구조를 벤다이어그 로 좌표 공간위에 표상로 전환 (추상적인 논리를 구체적인 위치 정보로 전환, Representatilon Shift), : 학생들은 추상적인 논리관계를 구체적인 공간정보로 바꾸면서 추상적 표현에 대한 방법과 원리를 이해할 수 있다.
높이값을 조절하면서 단순한 색상만로 구분하기 어려운 영역을 3D화하여 물리적로 느낄

수 있도록 하여 감각적인 확장로 유도시킬 수 있다.

파라메트릭 디자인방법론을 통해 집합의 개수를 조절하거나 복잡한 논리를 수학적인 규칙로 재구성하여 학생들이 수학적 규칙에 대해 표항적인 구조를 생성하면서 그 원리를 이해하도록 돕는다.

파라메트릭 디자인방법을 수학 교육에 적용하는 것은 입력값이 바뀌면 구조가 바뀌는 결과를 즉 각적로 관찰할 수 있도록 하여 수학적 원리를 동적 표상로 전환시켜 그 이해를 돕는다. 구 조가 변하는 것를 직접 눈로 관찰하여 연산중심이 아니라 연계성(Relation Thinking)을 중심

로 사고할 수 있도록 도울 수 있다. 이는 조건분석, 표현, 구조파악 능력을 강화할 수 있고 추 상적인 언어인 수학적 표현을 시각적로 극대화 하여 인지부하를 줄이며 정보를 즉각적로 해 석할 수 있도록 돕는 강력한 수단이라고 할 수 있을 것이다.

BeeGraphy는 수학의 자유로움을 실현하는 현대적인 도구가 아닐까?

이 내용은 다음 링크에서 실행해 볼 수 있습니다(데모)

BEEGRAPHY DEMO

BeeGraphy의 단계별 튜토리얼

위 구조를 만드는 과정을 단계별로 아래에 정리했다. (참고용)

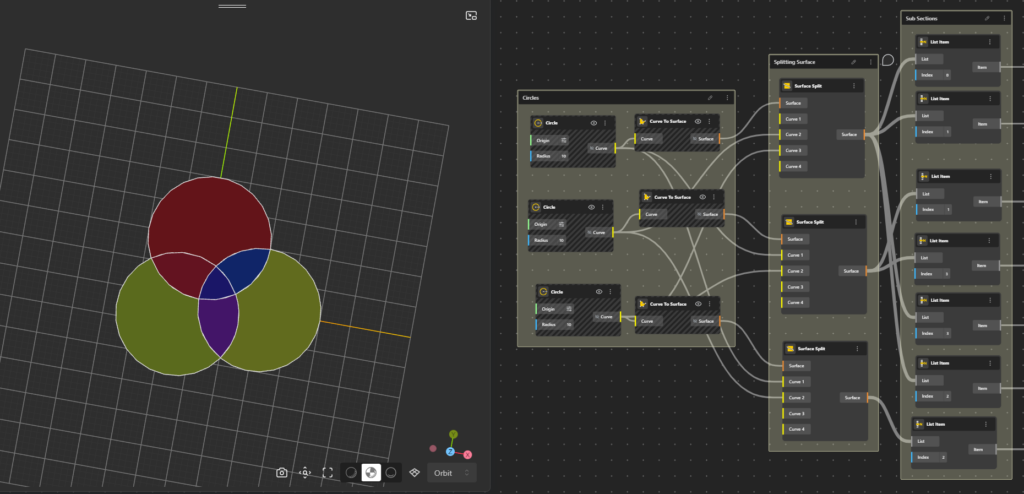
단계: 세ㅔ 개의 원을 만들고 이를 면(surface)로 변환하여 음영 처리된 작업 영역을 확보
단계: 서피스스필릿(Surface Split)을 이용해 각 원을 다른 파티션로 나누기 (예; 원 A의 교 차 영역을 구분하고 싶면 원 B와 C를 Curve 노드블록의 Input에 연결하고 원A를 Surface 노드블록에 연결)원 B와 C에 대해서도 동일한 방법을 반복하여 고유한 교차 영역을 확보하기
단계: 각 구역을 쉽게 구분하기 위해 List Item노드블록을 사용하여 각 영역에 인덱스를 부여 하기. (각 파티션을 개별적로 쉽게 찾을 수 있다)
단계: 각 구역에 Centroid노드블록을 이용해 점을 찍고,, 각 영역과 점을 1:1로 연결하기 (원 이 교차하면서 만들어지는 7개의 영역을 확보)
단계: 원 밖에 추가로 점 하나를 더 찍어 8번째 영역을 나타내기 (어떤 영역과도 겹치지 않도 록 점을 배치하는 것이 중요) ,, Interpolate노드블록을 이용해 점과 점을 연결하여 모든 영역을 통과하는 4번째 영역(집합)을 만들기.
단계: 각 영역의 정보와 상호작용이 용이하도록 모든 구역의 리스트를 만들고 List 노드의 입력 포트에 연겷하기. (여러개를 선택하려면 Shift를 누른 채 Item의 출력포트에서 List 노드로 와이 어를 드래그 하기)
단계: 인덱스 범위를 만들기 (Range Input노드를 추가하고 다음과 같이 설정하기)
- Min: 0
- Max: 6 (7개의 면이 있기 때문에 인덱스는 0부터 6까지 총 7개가 작동)
- Step Count: 1
- 노드 이름을 Input로 바꾸고 Index포트에 연결
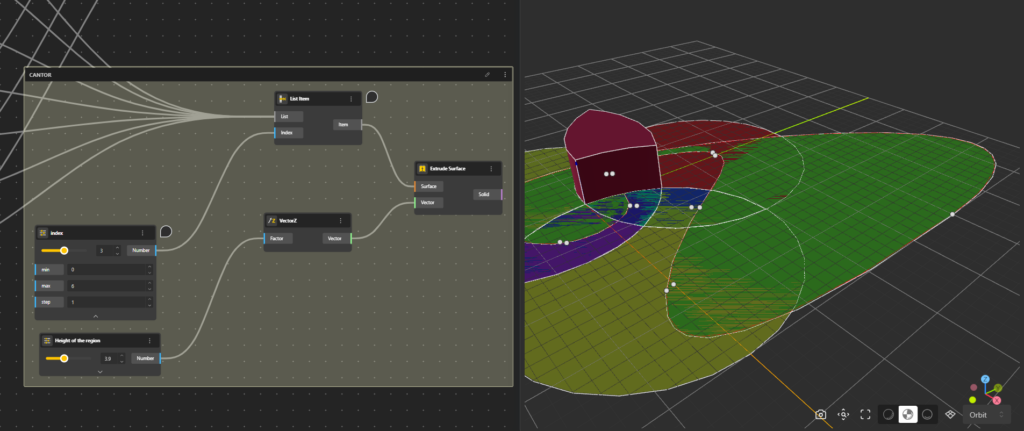
단계: Extrude Surface 노드를 추가하고 List Item출력을 Surface입력에 연결하기 (Range 범위에서 어떤 영역이던 자유롭게 선택 가능)
단계:돌출시킬구역의높이를조절하려면VectorZ를추가하고RangeInput노드블록에연결하기(슬라이더를이용해돌출시킬높이를조절할수있음)
단계: 모든 설정이 끝나면 DEMO(오른쪽 상단)로 이용하여 상호작용이 가능한 프레젠테이 션 공간에서 슬라이더 조절바를 이용해 수치를 바꿔가면서 이 구조를 이해할 수 있음.위 데모는 다음 링크에서 실행할 수 있다.